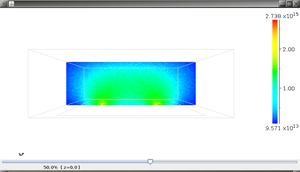
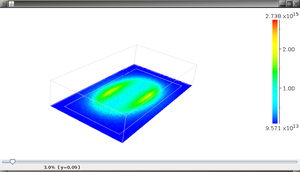
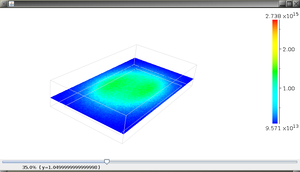
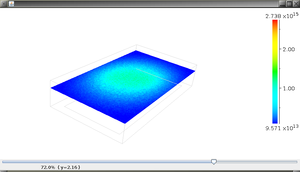
マグネトロンスパッタ装置 3次元解析

計算条件

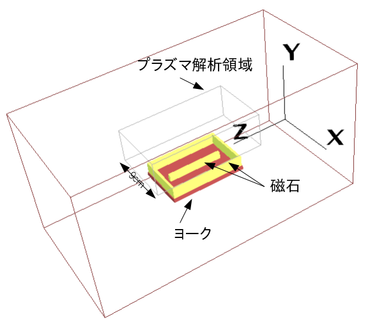
DCマグネトロンスパッタ装置
永久磁石の残留磁束密度 1.0[T], ターゲット表面の、ターゲット平行方向の磁束密度 500[G]
アルゴン、ガス圧 0.5[Pa]
印加電圧 Vdc = -300[V]
3次元カーテシアン直交座標系でモデル化

計算結果

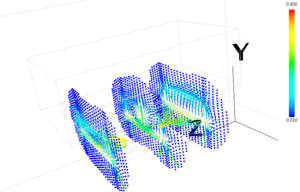
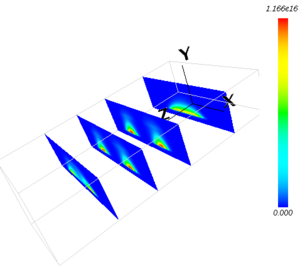
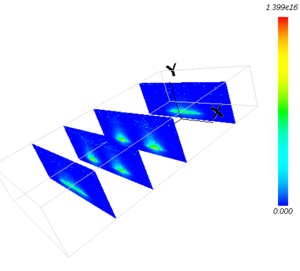
磁束密度分布
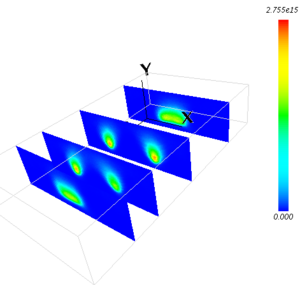
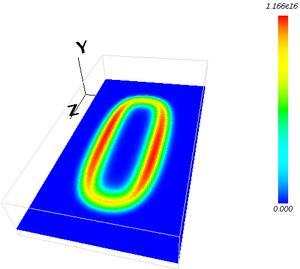
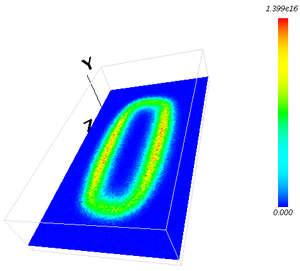
電子密度分布(xy面)
電子密度分布(xz面)
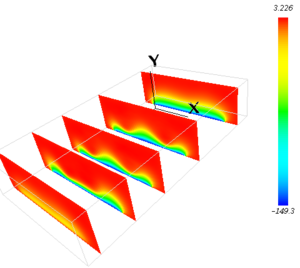
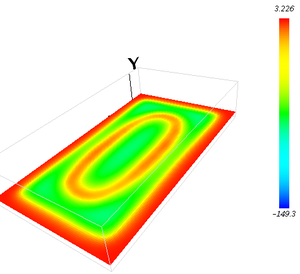
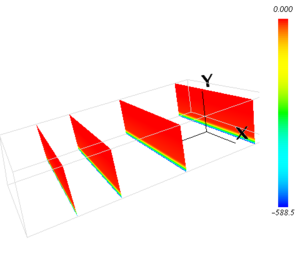
電位分布(xy面)
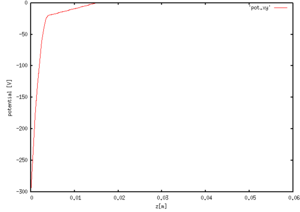
電位分布(xz面)
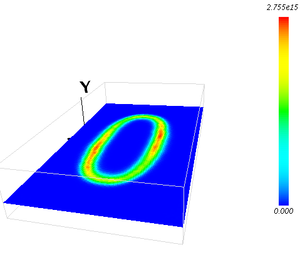
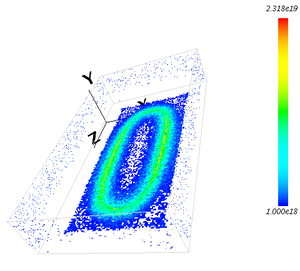
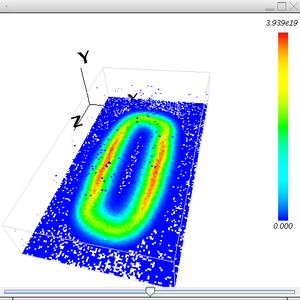
イオン密度分布(xy面)
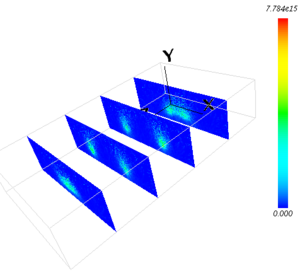
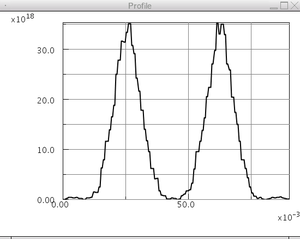
イオンフラックス分布
イオンフラックス分布
電子密度分布(xy面)
電子密度分布(xz面)
与えた電位分布(xy面)
与えた電位分布(y方向)
イオン密度分布(xy面)
イオン密度分布(xz面)
イオンフラックス分布
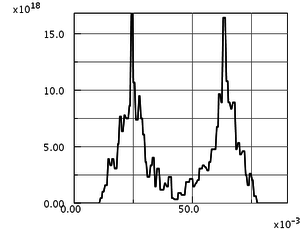
Al密度分布1
Al密度分布2
Al密度分布3
Al密度分布4

MSSM3D により永久磁石による磁束密度分布を計算します。次に、その静磁場中での荷電粒子の運動を PIC-MCCM3D により追跡し、プラズマ密度分布やターゲットへのイオンフラックス、イオンのエネルギーなどを評価します。さらに DSMCM 3D によって、スパッタ粒子の輸送計算を行い、基板に到達するスパッタ粒子のフラックス分布を得ます。

MSSM3D による3次元静磁場解析
・50x80x80 分割程度
・計算時間は Core2Duo 3.8GHz の計算機で 5分程度

PIC-MCCM3D による 3次元プラズマ解析
3次元プラズマ解析は、計算時間やメモリ量がかなりかかります。Gbyte オーダーのメモリが必要になるため、64bit の計算機を使用することを推奨します。また、プラズマ現象は本質的に非線形であるため、メッシュを細かく切らないと計算が発散するといった問題もあります。そこで今のところ、次の2 つの計算手法をオプションとして選択して頂くことにしました。

1. 通常の PIC/MCC アルゴリズムによる解析
電子とイオンの運動は、電位分布を通してカップリングしており、Self-consistent な電子、イオン、電位分布が得られます。
ポアソン方程式を毎ステップ解くため、計算時間がかかります。
メッシュ分割幅や、超粒子数の条件によっては計算が破綻します。

2. 電位分布を外部から与えて、固定した解析
電位分布が固定されているため、電子とイオンの運動はカップリングしておらず、電子とイオンの密度のバランスがとれません。相対的な分布は、与える電位分布に依存しますがそれなりに妥当なものが得られるようです。絶対値については電流値やパワーなどから間接的に評価する必要があります。
ポアソン方程式を解かない分、計算時間は短くてすみます。
メッシュが粗くても、計算が破綻することはあり得ません。

1. のやり方はごく通常の PIC/MCC アルゴリズムによる計算で、 Self-consistent な計算結果が得られるという利点がありますが、相当メッシュを細かく切らないと計算が破綻しがちです。 2. のやり方は、結果の妥当性についての検証は必要ですが、計算が破綻することがあり得ないという強力な利点があります。以下に、1. と 2. の計算方法での結果を示します。

DSMCM 3D による、スパッタ粒子の輸送計算
PIC-MCCM 3D の計算結果でターゲットへの入射イオンフラックス分布が得られます。ターゲットを Al としてスパッタリング率を 1.0、スパッタ粒子の放出エネルギーを 10eVと仮定し、スパッタ粒子の放出フラックスを与えました。スパッタ粒子の移動、衝突過程を DSMCM 3D で追跡することにより、基板へ堆積するスパッタ粒子のフラックス分布を得ることが出来ます。