イオン化スパッタリング
計算条件
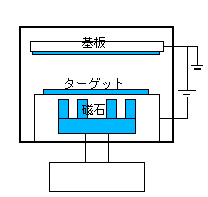
- DCマグネトロンスパッタ装置
- 永久磁石の残留磁束密度 0.5[T], ターゲット表面の、ターゲット平行方向の磁束密度 300[G]
- アルゴン、ガス圧 5[mTorr]
- ターゲットの材質 銅
- ターゲットの印加電圧 Vdc = -600[V]
- 基板に -200[V] の負の電圧を印加
- 2次元円筒座標系でモデル化
計算結果
-
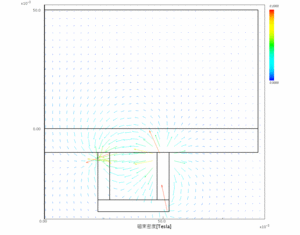
磁束密度分布
-
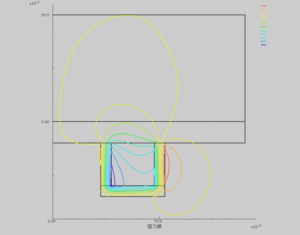
磁力線
-
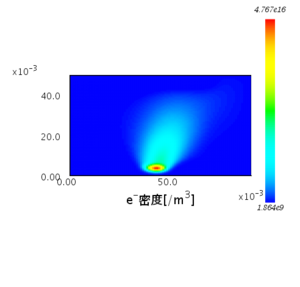
電子密度分布
-
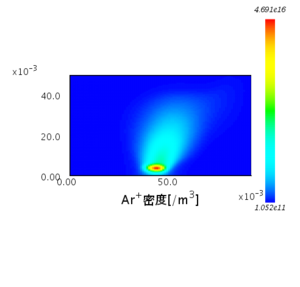
Ar+ 密度分布
-
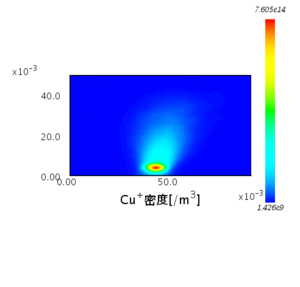
Cu+ 密度分布
-
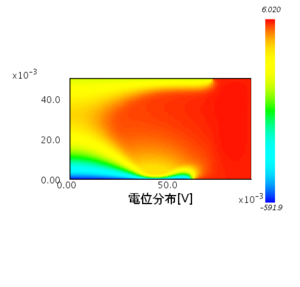
電位分布
-
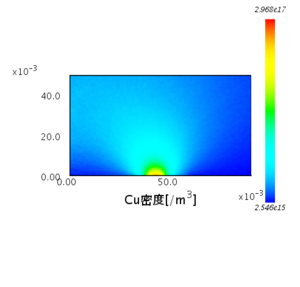
Cu 密度分布
-
Cu フラックス
-
Cu と Cu+ 基板への入射角度分布 r=0.0[cm]
-
Cu と Cu+ 基板への入射角度分布 r=3.0[cm]
-
Cu と Cu+ 基板への入射角度分布 r=6.0[cm]
イオン化スパッタリングを考慮にいれた解析例です。 マグネトロンスパッタ装置内の解析 と似ている計算体系です。スパッタ粒子のイオン化を考慮するために PIC-MCCM によるプラズマ解析と DSMCM によるスパッタ粒子の挙動解析をカップリングして計算している点が異っています。
Step 1 静磁場解析
磁石や磁性体の配置、磁石の強度(残留磁束密度)を条件として与えて、装置内の磁束密度分布を計算します。
Step 2 スパッタ粒子の放出角度分布、エネルギーの推測
予備計算を行うなどして、Arイオンのターゲットへの入射エネルギーを推測しておきます。 電極の Vdc と同程度と考えて良いでしょう。また、SASAMALを用いた計算を行うか文献を参照するなどして、 スパッタ粒子の放出角度分布、エネルギーを推測しておきます。ここでは放出角度分布は余弦則に従い、 放出エネルギーは 10eV であると仮定しました。
Step 3 プラズマ/スパッタ粒子のカップリング計算
PIC-MCCM によるプラズマ計算では、
・静磁場(MSSMの計算結果)
・電場(電極や荷電粒子自身の密度分布から決まる)
・気体分子(Ar)やスパッタ粒子(Cu)の、電子との電離衝突や弾性散乱など
・イオン(Ar+, Cu+) と中性粒子(Ar,Cu)の弾性衝突など
などを考慮に入れて荷電粒子(電子、Ar+, Cu+)の運動を追跡します。DSMCM によるスパッタ粒子の挙動解析では
・ターゲットに入射するイオンフラックスに応じて、スパッタ粒子(Cu) をターゲットから放出する
・気体分子(Ar)やスパッタ粒子(Cu)との弾性散乱
を考慮にいれてスパッタ粒子(Cu) の運動を追跡します。PIC-MCCM の計算とDSMCM の計算を、セルフコンシステントな定常状態が得られるまで交互に繰り返します。


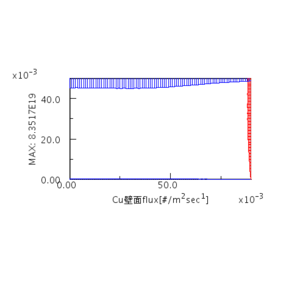
![Cu と Cu+ 基板への入射角度分布 r=0.0[cm]](http://www.psinc.co.jp/assets_c/2015/05/ang_1-thumb-300xauto-81.gif)
![Cu と Cu+ 基板への入射角度分布 r=3.0[cm]](http://www.psinc.co.jp/assets_c/2015/05/ang_2-thumb-300xauto-82.gif)
![Cu と Cu+ 基板への入射角度分布 r=6.0[cm]](http://www.psinc.co.jp/assets_c/2015/05/ang_3-thumb-300xauto-83.gif)